Convexity - the obscure metric every smart investor swears by

Abraham George Market Musings

Convexity is not a common word that we equity analysts use everyday. It is part of bond math. The equivalent of that is gamma in options. In practical terms, convexity is the second derivative of an instrument or a sexy way of being aware of the added risk that you normally do not account for. In plain terms, it measures the curvature of a line or the acceleration of an object. If this sounds Greek to you, rest assured that it is indeed.

The second derivative is everywhere in finance. Once you start seeing it you can’t unsee it. In many cases it is measurable and known but in most cases it is hidden. Once you are aware of it, you will be always looking for it. When some one blows up in the financial world, it’s usually a failure to understand the second derivative. It’s like saying I know my exposure here but I don’t know what is it over there.

The first thing to understand is that stocks have convexity. Inherently some stocks are positively convex and other stocks are negatively convex. To better understand this is to think a positively convex stock goes up faster than it comes down. A negatively convex stock goes down faster than it goes up. A lot of stocks, like the banks were negatively convex in 2008. The banks sold a great deal of optionality, which turned them into vehicles of negative convexity. They went up slowly but came down fast, which is roughly the payoff of a short option. Citibank and Lehman brothers were classic examples. If you really understood the seriousness of what was going on in the mortgaged back securities, you could have protected yourself from your investments in Citibank or Lehman if you had any. In India the classic equivalents were Yes bank and PNB.

In general tech stocks and biotech stocks are positively convex. But there are exceptions. And there are positively convex stocks in plenty of other industries including retail, energy and mining. This doesn’t mean you cannot have a negatively convex stock in your portfolio, but on balance your portfolio should be positively convex. If bad things happen to the market, you want good things to happen to you.

Take the case of Tanla or even Subex, it is clear it has positive convexity. Ever since it broke above the 14-year consolidation and positive news started rolling out, every pullback has been shorter than how much it travels higher. We also need to understand that stocks have embedded convexity. If you look at a chart, it seems straight forward. It goes up and down. But sometimes it can go up and down rapidly. Convexity can fool you as well because we think in linear ways and many times it will turn non-linear and can hurt you in a bad way. It’s a complicated concept to grasp.

Those who are invested in Tanla are very frustrated at the moment. They are very focused on charts and have abandoned all fundamental analysis. The basic premise of fundamental analysis is the stock’s real price is the present value of future cash flows. Instead of looking at where all value is being added and what could be the intrinsic value the focus is all on price based on your point of entry. Prices did not break above 1030 and now it has broken below 780 which was a critical chart point, and now it has to go to 570. If you believe that strongly ignoring all other fundamental factors why don’t you take action based on what you see on the charts.

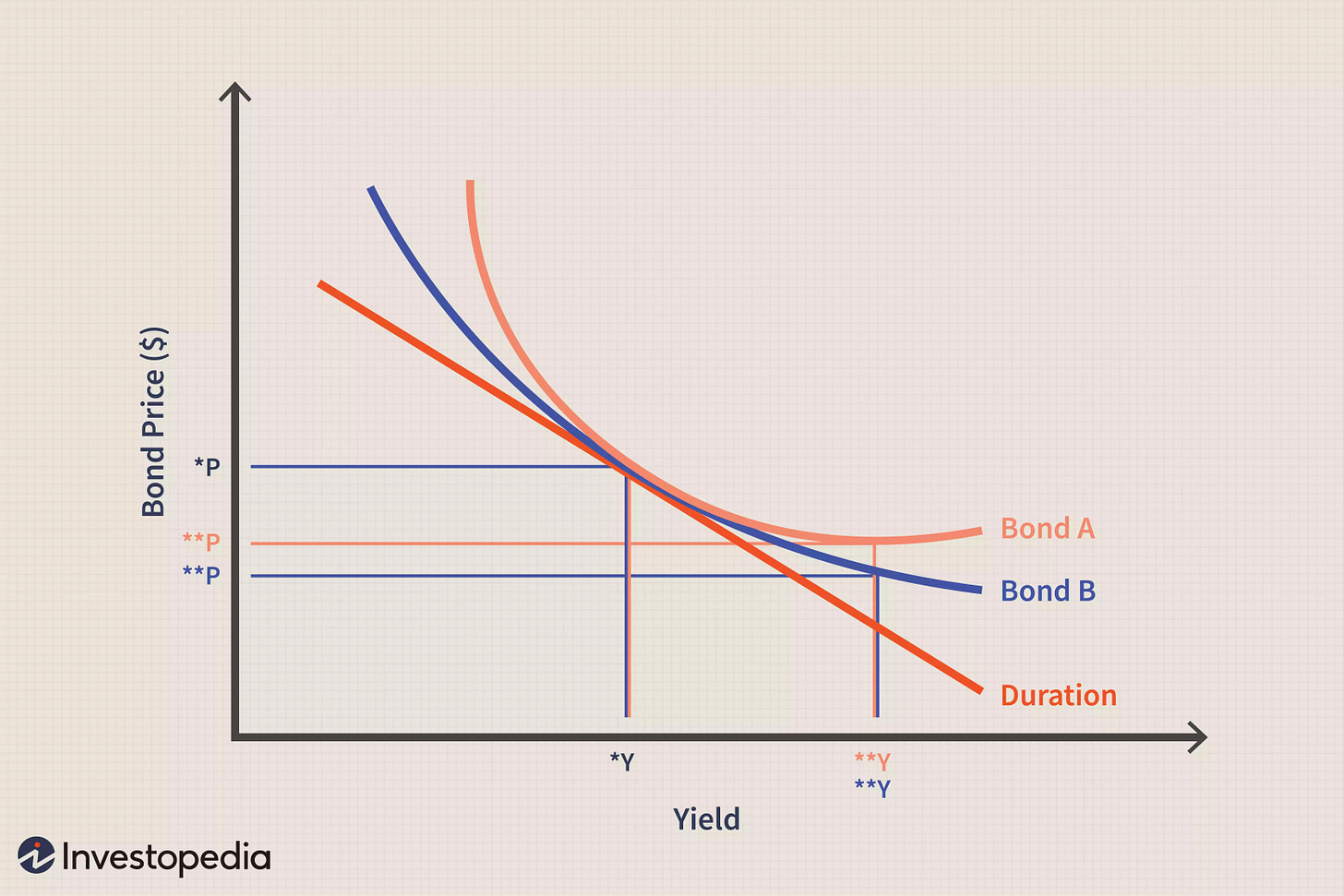
Convexity is much more measurable in bonds. If you are invested in high yield bonds, you come to a point that high yields can’t go up much more but it has the risk of going down a lot meaning it has negative convexity. The coupon you get for high yield bonds is the premium you get for selling options. If the Fed is not active the premium could be large and bonds can become more attractive. People who understand income investing know intuitively about the negative convexity present in these strategies.

One of the tragedies of zero interest rate policy is that it has forced retirees to load up on negative convexity in search of income, unusually in the form of corporate bonds and high dividend stocks. If you don’t manage this properly, it will turn out to be something like collecting pennies in front of a steamroller. Understanding convexity is fundamental to any portfolio manager. Once you start thinking about your portfolio in terms of convexity, your outcomes will improve. Not just returns but risk adjusted returns.

Abraham George is a seasoned investment manager with more than 40 years of experience in trading & investment and portfolio management spanning diverse environments like banks (HSBC, ADCB), sovereign wealth fund (ADIA), a royal family office and a hedge fund.